En muchas situaciones suele ser conveniente generar un conjunto de variables con una correlación deseada. Algunos paquetes ofrecen medios para este fin de producir fake data; pero también es perfectamente posible obtenerlas a través de métodos como la factorización (descomposicion) de Cholesky o la Descomposicion del Valor Singular (SVD: Singular Value Decomposition). En el paquete de base de R existen funciones para hacer estos cálculos.
La factorización de Cholesky, es un método con el que una matriz definida positiva y simetrica, es descompuesta en el producto de dos matrices triangulares (triangular inferior o superior)
Mientras que la SVD (descomposición de valor singular) es una factorización de la forma:
La implementación consiste simplemente en obtener el producto entre un vector de variables independientes entre si y el factor obtenido por el procedimiento de Cholesky o SVD. El código que sigue, con muy ligeras variantes, sigue la forma de una respuesta que ví en StackOverflowhace algún tiempo; lo que me propongo es comprobar que en efecto se producen las variables correlacionadas, y explorar el por qué.
Con esto se construye una matriz de 3 variables sin asociación lineal entre si. Ahora con la función outeres posible obtener una matriz con las correlaciones deseadas supongamos .9 y .8
Como puede observarse solo se utilizará del SVD la matriz cuadrada obtenida de
La sección correspondiente a Cholesky es analoga
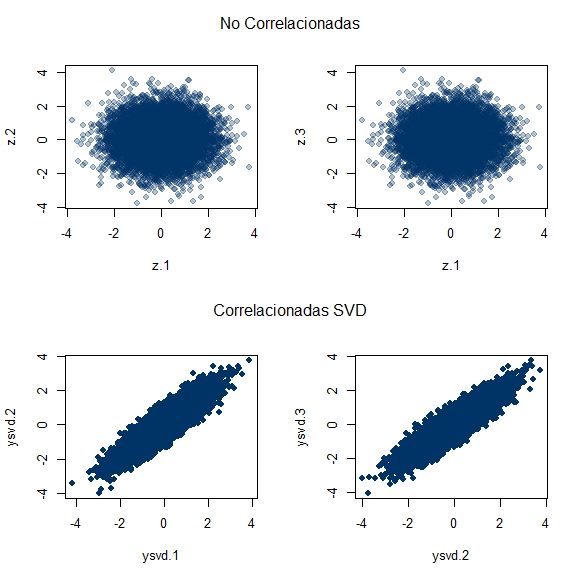
Para visualizar esto:
Los resultados de Cholesky, se pueden ver abajo:
Visual o esteticamente, no es nada impactante claro, pero si se puede apreciar que de un vector de variables independientes es posible generar o simular un conjunto de variables correlacionadas. Funciona porque: Z ~ N(0, 1) & Y = QZ; la matriz de varianzas y covarianzas es E(YY') = E(QZZ'Q') = QE(ZZ')Q' = QQ' dado que: E(ZZ') = I.
También si vemos la siguiente figura:
El gráfico, realmente no es muy eficaz en mostrar a primera vista la diferencia en la dispersion; sin embargo, si uno presta atención a los ejes horizontales, notará que, en efecto, existen diferencias entre las varianzas, lo que recuerda la afirmación según la cual, 'la media de un crecido numero de cantidades altamente correlacionadas, tendrá mas alta varianza que la media de un crecido número de cantidades no correlacionadas'-lo cual puede marcar la diferencia entre la validacion cruzada y la LOOCV-; dicha afirmación se encuentra en el libro Introduction to Statistical Learning de James, Witten, Hastie y Tibshirani
Las correlacionadas son casi el doble o triple en varianza, en este caso al menos.
La factorización de Cholesky, es un método con el que una matriz definida positiva y simetrica, es descompuesta en el producto de dos matrices triangulares (triangular inferior o superior)
A = LL' (L es una matriz triangular inferior) A = U'U (U es una matriz triangular superior) siendo U' la traspuesta de U
Mientras que la SVD (descomposición de valor singular) es una factorización de la forma:
A = UΣV, la cuál generaliza la descomposición de autovalores.
La implementación consiste simplemente en obtener el producto entre un vector de variables independientes entre si y el factor obtenido por el procedimiento de Cholesky o SVD. El código que sigue, con muy ligeras variantes, sigue la forma de una respuesta que ví en StackOverflowhace algún tiempo; lo que me propongo es comprobar que en efecto se producen las variables correlacionadas, y explorar el por qué.
sims <- 10000 rs <- 3 n <- rs * sims # 30mil simulaciones set.seed(45) z <- matrix(rnorm(n), nrow = 3) # una matriz con 3 variables
Con esto se construye una matriz de 3 variables sin asociación lineal entre si. Ahora con la función outeres posible obtener una matriz con las correlaciones deseadas supongamos .9 y .8
r <- .9 rho <- outer(seq(3), seq(3), function(i, j) r^abs(i - j)) # matriz 3x3 de correlacionesCon la funcion base::svd se obtiene la descomposicion de valor singular; mientras que base::chol permite la la factorización de Cholesky (el valor resultante es una matriz triangular superior)
dec_svd <- svd(rho) names(dec_svd) # [1] "d" "u" "v" d <- dec_svd[["d"]] d <- diag(d) # extracción de la diagonal d <- sqrt(d) # raiz cuadrada v <- dec_svd[["v"]] # autovector R <- tcrossprod(v, d)# producto matricial
Como puede observarse solo se utilizará del SVD la matriz cuadrada obtenida de
V√D
La sección correspondiente a Cholesky es analoga
# Cholesky factorization chol_dec <- chol(rho) x <- colMeans(z) ysvd <- colMeans(R %*% z) ychol <- colMeans(chol_dec %*% z)
Para visualizar esto:
# PLOT SVD-------------------------------------------------
# NO CORRELACIONADAS VS SVD
par(mfrow = c(2, 2))
plot(t(z)[, 1:2], pch = 19, col = scales::alpha("#003366", .3),
xlab = "z.1", ylab = "z.2")
plot(t(z)[,1:3], pch = 19, col = scales::alpha("#003366", .3),
xlab = "z.1", ylab = "z.3")
mtext("NO CORRELACIONADAS", outer = TRUE, side = 3, line = -2)
plot(t(R %*% z)[, 1:2], pch = 19, col = "#003366",
xlab = "ysvd.1", ylab = "ysvd.2")
plot(t(R %*% z)[, 2:3], pch = 19, col = "#003366",
xlab = "ysvd.2", ylab = "ysvd.3")
mtext("CORRELACIONADAS\nSVD", outer = TRUE, side = 3, line = -21)Los resultados de Cholesky, se pueden ver abajo:
par(mfrow = c(2, 2))
plot(t(z)[, 1:2], pch = 19, col = scales::alpha("#003366", .3),
xlab = "z.1", ylab = "z.2")
plot(t(z)[,1:3], pch = 19, col = scales::alpha("#003366", .3),
xlab = "z.1", ylab = "z.3")
mtext("NO CORRELACIONADAS", outer = TRUE, side = 3, line = -2)
plot(t(chol_dec %*% z)[, 1:2], pch = 19, col = scales::alpha("#003366", .8),
xlab = "ychol.1", ylab = "ychol.2")
plot(t(chol_dec %*% z)[, 2:3], pch = 19, col = scales::alpha("#003366", .8),
xlab = "ychol.1", ylab = "ychol.3")
mtext("CORRELACIONADAS\nCHOLESKY", outer = TRUE, side = 3, line = -21)
Visual o esteticamente, no es nada impactante claro, pero si se puede apreciar que de un vector de variables independientes es posible generar o simular un conjunto de variables correlacionadas. Funciona porque: Z ~ N(0, 1) & Y = QZ; la matriz de varianzas y covarianzas es E(YY') = E(QZZ'Q') = QE(ZZ')Q' = QQ' dado que: E(ZZ') = I.
También si vemos la siguiente figura:
par(mfrow = c(2, 2))
plot(t(z)[, 1:2], pch = 19, col = scales::alpha("#003366", .3),
xlab = "z.1", ylab = "z.2")
plot(t(z)[,1:3], pch = 19, col = scales::alpha("#003366", .3),
xlab = "z.1", ylab = "z.3")
mtext("NO CORRELACIONADAS", outer = TRUE, side = 3, line = -2)
plot(t(R %*% z)[, 1:2], pch = 19, col = "#003366",
xlab = "ysvd.1", ylab = "ysvd.2")
plot(t(R %*% z)[, 2:3], pch = 19, col = "#003366",
xlab = "ysvd.2", ylab = "ysvd.3")
mtext("CORRELACIONADAS\nSVD", outer = TRUE, side = 3, line = -21)
El gráfico, realmente no es muy eficaz en mostrar a primera vista la diferencia en la dispersion; sin embargo, si uno presta atención a los ejes horizontales, notará que, en efecto, existen diferencias entre las varianzas, lo que recuerda la afirmación según la cual, 'la media de un crecido numero de cantidades altamente correlacionadas, tendrá mas alta varianza que la media de un crecido número de cantidades no correlacionadas'-lo cual puede marcar la diferencia entre la validacion cruzada y la LOOCV-; dicha afirmación se encuentra en el libro Introduction to Statistical Learning de James, Witten, Hastie y Tibshirani
m <- cbind(No_corr = x, SVD = ysvd, CHOL = ychol) apply(m, 2, var) # No_corr SVD CHOL # 0.3371519 0.9045895 0.6170597
Las correlacionadas son casi el doble o triple en varianza, en este caso al menos.



Comentarios
Publicar un comentario